程序开发实训 【专题三】 指针
包含题目
1、求最小数和次小数的位置
2、求平均值与标准差
3、矩阵替换
4、矩阵转置
5、数组排序
6、求最大公约数或最小公倍数
注意
1.以下代码仅供参考,不代表最优解。
2.代码的运行结果与编译环境有关,以下代码均通本地测试,如果代码存在无法编译或输出异常,请检查运行环境。
3.如果发现问题或者您有更优的解,欢迎加群交流。
# 指针作为函数的参数
# 1、求最小数和次小数的位置
【问题描述】
给定一个整型数组,编程求该数组中最小数和次小数首次出现的位置,也就是说数组中重复出现的数值按等值处理。
【输入形式】数组中数值的个数 n 和 n 个整数。
【输出形式】最小数和次小数在数组中的位置(中间用空格隔开),如果找不到次最小值,则输出-1。
【样例输入】
5
89 43 14 8 8
【样例输出】3 2
#include <iostream>
#include <stdio.h>
using namespace std;
int firMinIndex = -1, secMinIndex = -1;
void findMin(int *pArr, int len)
{
int firstMin = 32767, secMin = 32767;
for (int i = 0; i < len; i++)
{
if (pArr[i] < firstMin)
{
secMin = firstMin;
secMinIndex = firMinIndex;
firstMin = pArr[i];
firMinIndex = i;
}
else if (pArr[i] < secMin && pArr[i] > firstMin)
{
secMin = pArr[i];
secMinIndex = i;
}
}
}
int main()
{
int n;
cin >> n;
int data[n];
for (int i = 0; i < n; i++)
cin >> data[i];
findMin(data, n);
cout << firMinIndex << " " << secMinIndex << endl;
return 0;
}
# 2、求平均值与标准差
【问题描述】
编写一个程序,输入若干个整数,利用动态分配申请相应大小的内存空间,计算并输出其均值与标准差。
(1)计算均值的公式:
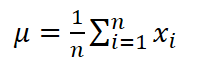
(2)计算标准差的公式:

【输入形式】
第一行一个整数 N,表示数据的个数。 第二行 N 个整数,表示各个整数,中间用空格隔开。
【输出形式】均值和标准差(中间用空格隔开,均保留两位小数)
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
void stat(int *x, int n, float &mu, float &delta)
{
float sum = 0.0;
for (int i = 0; i < n; i++)
sum += x[i];
mu = sum / n;
sum = 0;
for (int i = 0; i < n; i++)
sum += pow(x[i] - mu, 2);
delta = sqrt(sum / n);
cout << fixed << setprecision(2) << mu << " " << delta << endl;
}
int main()
{
int N;
float mu = 0.0, delta = 0.0;
cin >> N;
int *a = new int[N];
for (int i = 0; i < N; i++)
cin >> a[i];
stat(a, N, mu, delta);
delete[] a;
return 0;
}
# 指针函数
# 3、矩阵替换
【问题描述】
先输入两个矩阵 A 和 B,然后输入替换位置(左上角),编写程序将矩阵 A 中从替换位置开始的子矩阵(与 B 同样大小)替换为 B,并输出替换后的矩阵。
【输入形式】
从控制台先输入矩阵 A 的行数和列数(行数和列数均大于等于 1,小于等于 20),然后在新的行上输入矩阵 A 的各行数字(以一个空格分隔的整数)。再以同样的方式输入矩阵 B。最后输入替换位置(用一个空格分隔的两个整数表示,行数和列数都从 1 开始计数,因此两个整数都大于等于 1)。若替换位置超出了矩阵 A 的行数或列数,则原样输出矩阵 A。
【输出形式】 在标准输出上分行输出替换后的矩阵,每行中各数字之间以一个空格分隔。
【输入样例 1】
5 6
10 2 34 -1 800 90
2 76 56 -200 23 1
35 0 0 98 8 3000
2000 100 -1 1 2 0
8 7 85 963 496 8
2 3
9 9 9
9 9 9
3 3
【输出样例 1】
10 2 34 -1 800 90
2 76 56 -200 23 1
35 0 9 9 9 3000
2000 100 9 9 9 0
8 7 85 963 496 8
#include <iostream>
#include <stdio.h>
using namespace std;
int **create(int row, int col)
{
// 动态开辟二维数组
int **arr = new int *[row + 1];
for (int i = 1; i <= row; i++)
arr[i] = new int[col + 1];
// 读入数据
for (int i = 1; i <= row; i++)
for (int j = 1; j <= col; j++)
cin >> arr[i][j];
// 返回指针
return arr;
}
int **solve(int **ptrA, int rowA, int colA, int **ptrB, int rowB, int colB, int row, int col)
{
int r, c;
for (int i = 1; i <= rowB; i++)
{
// 重置列
c = col;
r = row++;
for (int j = 1; j <= colB; j++)
{
if (r <= rowA && c <= colA)
ptrA[r][c++] = ptrB[i][j];
}
}
return ptrA;
}
void show(int **p, int row, int col)
{
for (int i = 1; i <= row; i++)
{
for (int j = 1; j <= col; j++)
cout << p[i][j] << " ";
cout << endl;
}
}
int main()
{
int rowA, colA;
cin >> rowA >> colA;
int **A = create(rowA, colA);
int rowB, colB;
cin >> rowB >> colB;
int **B = create(rowB, colB);
int row, col;
cin >> row >> col;
A = solve(A, rowA, colA, B, rowB, colB, row, col);
show(A, rowA, colA);
return 0;
}
# 4、矩阵转置
【问题描述】
从键盘上输入一个 n*n 的整型二维矩阵,存放在一个二维整型数组。要求写一个函数 transpostion 实现二维数组的转置。所谓转置,就是就行矩阵元素的行号和列号的对换,也就是第 i 行第 j 列的数据和第 j 行第 i 列的数据交换位置。完成转置操作后,写一个函数 show,实现二维数组的输出。每个数字占 5 个字符宽度,同行中每个数据之间用空格隔开,在每一行末均输出一个回车符。
【输入形式】
第一行输入 N,表示矩阵的行/列数。 接下来 N 行,第 i 行共 N 个数据,表示第 i 行的数据。
【输出形式】N 行 N 列。逆置后的二维数组。
【样例输入】
3
1 2 3
4 5 6
7 8 9
【样例输出】
1 4 7
2 5 8
3 6 9
#include <iostream>
#include <iomanip>
using namespace std;
int **create(int row, int col)
{
int **arr = new int *[row + 1];
for (int i = 0; i < row; i++)
arr[i] = new int[col + 1];
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> arr[i][j];
return arr;
}
void transpostion(int **p, int n)
{
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
swap(p[i][j], p[j][i]);
}
void show(int **p, int row, int col)
{
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
cout << p[i][j] << " ";
cout << endl;
}
}
int main()
{
int n;
cin >> n;
int **pA;
pA = create(n, n);
transpostion(pA, n);
show(pA, n, n);
return 0;
}
# 函数指针
# 5、数组排序
【问题描述】
给定一个整型一维数组,编程实现对该数组的排序。其中输入 1 时,表示对该数组按升序排序;如果输入是 0,表示对该数组按降序排序。最后输出排序结果。
【输入形式】
数组中数值的个数 n,以及 n 个整型数据。 最后一行输入排序规则,其中输入 1 时,表示排序规则是升序;输入 0 时,表示排序规则是降序。
【输出形式】排序结果。
【样例输入】
10
39 37 46 86 93 64 4 7 88 27
1
【样例输出】
4 7 27 37 39 46 64 86 88 93
#include <iostream>
#include <stdio.h>
using namespace std;
void sortArr(int arr[], int len, int (*compare)(int, int));
int ascending(int a, int b);
int descending(int a, int b);
int main()
{
int n;
cin >> n;
int data[n];
for (int i = 0; i < n; i++)
cin >> data[i];
int order; //order=1是升序;order=0是降序
cin >> order;
int (*pFun)(int, int); //声明一个函数指针
if (order == 1)
pFun = ascending;
else
pFun = descending;
sortArr(data, n, pFun);
for (int i = 0; i < n; i++)
cout << data[i] << " ";
cout << endl;
return 0;
}
void sortArr(int arr[], int len, int (*compare)(int, int))
{
for (int i = 0; i < len - 1; i++)
for (int j = 0; j < len - 1 - i; j++)
if (!compare(arr[j], arr[j + 1]))
swap(arr[j], arr[j + 1]);
}
int ascending(int a, int b)
{
return a < b;
}
int descending(int a, int b)
{
return a > b;
}
# 6、求最大公约数或最小公倍数
【问题描述】
从键盘上输入 2 个正整数,计算这两个正整数的最小公倍数或者最大公约数。其中输入 1 时,输出两个正整数的最大公约数;如果输入是 2,输出两个正整数的最小公倍数。。 提示: 公式 lcm = a * b / gcd(a,b)
【输入形式】
第一行,两个正整数,中间用空格隔开。 第二行一个整数,表示选择项。
【输出形式】一个整数,表示输入数据的最小公倍数或者最大公约数。
【样例输入】
12 18
2
【样例输出】36
// 函数指针-求最小公倍数或最大公约数
#include <iostream>
using namespace std;
int gcd(int a, int b)
{
// 最大公约数
int temp;
while (b)
{
temp = a % b;
a = b;
b = temp;
}
return a;
}
int lcm(int a, int b)
{
// 最小公倍数
return a * b / gcd(a, b);
}
int main()
{
int a, b;
int choice;
int (*pFun)(int, int);
cin >> a >> b;
cin >> choice;
choice == 1 ? pFun = gcd : pFun = lcm;
cout << (*pFun)(a, b);
return 0;
}
# 评论交流
最后,如果你觉得笔记对你有帮助,不妨赞赏一杯可乐😅
QQ 交流群 217394861

