树和树的算法(一)
# 目标
- 要理解树数据结构是什么,以及如何使用它。
- 查看树如何用于实现 map 数据结构。
- 使用类和引用来实现树。
- 实现树作为递归数据结构。
- 使用堆实现优先级队列。
# 树的例子
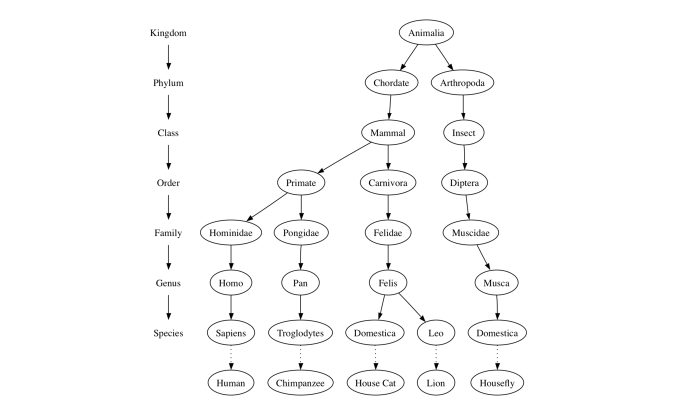
- 生物学的分类树(图一)
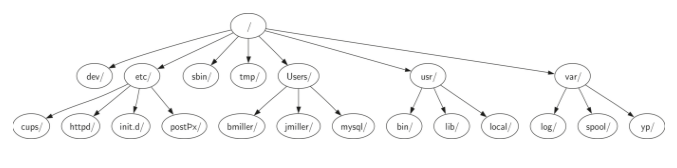
- Unix文件系统层次结构的一小部分(图二)
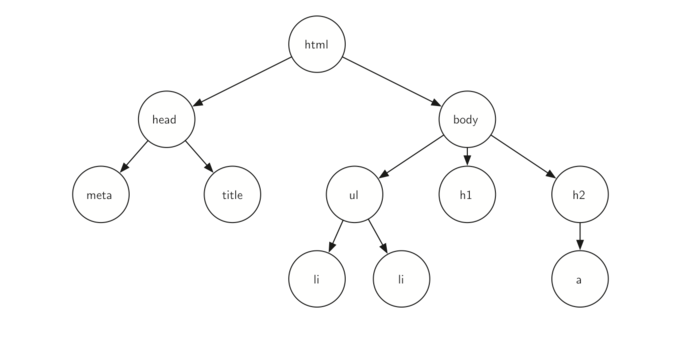
- HTML编写的简单网页(图三)
# 名词和定义
# 节点(Node)
节点是树的基本部分。它可以有一个名称,我们称之为“键”。节点也可以有附加信息。我们将这个附加信息称为“有效载荷”。虽然有效载荷信息不是许多树算法的核心,但在利用树的应用中通常是关键的。
# 边(Edge)
边是树的另一个基本部分。边连接两个节点以显示它们之间存在关系。每个节点(除根之外)都恰好从另一个节点的传入连接。每个节点可以具有多个输出边。
# 根(Root)
树的根是树中唯一没有传入边的节点。在 (图二)中,/ 是树的根。
# 路径(Path)
路径是由边连接节点的有序列表。例如,(图一)中 Mammal→Carnivora→Felidae→Felis→Domestica 是一条路径。
# 子节点(Children)
具有来自相同传入边的节点 c 的集合称为该节点的子节点。在 (图二)中,节点 log/,spool/ 和 yp/ 是节点 var/ 的子节点。
# 父节点(Parent)
具有和它相同传入边的所连接的节点称为父节点。在(图二)中,节点 var/ 是节点 log/,spool/ 和 yp/ 的父节点。
# 兄弟节点(Sibling)
树中作为同一父节点的子节点的节点被称为兄弟节点。节点 etc/ 和 usr/ 是文件系统树中的兄弟节点。
# 子树(Subtree)
子树是由父节点和该父节点的所有后代组成的一组节点和边。
# 叶节点(Leaf Node)
叶节点是没有子节点的节点。 例如,人类和黑猩猩是 (图一) 中的叶节点。
# 层数(Level)
节点 n 的层数为从根结点到该结点所经过的分支数目。 例如,(图一)中的Felis节点的级别为五。根据定义,根节点的层数为零。
# 高度(Height)
树的高度等于树中任何节点的最大层数。(图二)中的树的高度是 2。
现在已经定义了基本词汇,我们可以继续对树的正式定义。 事实上,我们将提供一个树的两个定义。 一个定义涉及节点和边。 第二个定义,将被证明是非常有用的,是一个递归定义。
定义一:树由一组节点和一组连接节点的边组成。树具有以下属性:
- 树的一个节点被指定为根节点。
- 除了根节点之外,每个节点 n 通过一个其他节点 p 的边连接,其中 p 是 n 的父节点。
- 从根路径遍历到每个节点路径唯一。
- 如果树中的每个节点最多有两个子节点,我们说该树是一个二叉树(BinaryTree)。
下图展示了适合定义一的树。边上的箭头指示连接的方向。
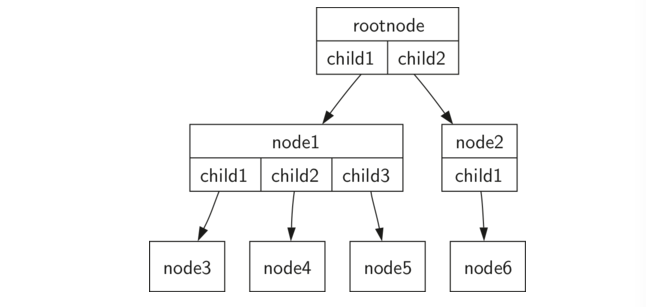
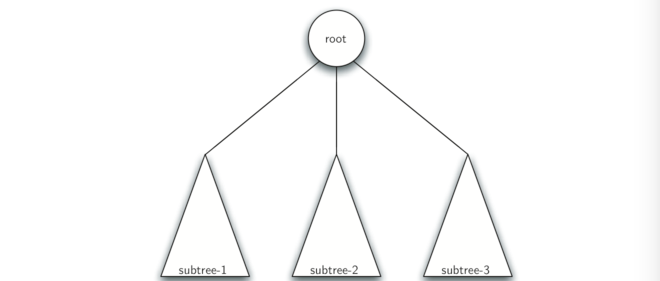
定义二:树是空的,或者由一个根节点和零个或多个子树组成,每个子树也是一棵树。每个子树的根节点通过边连接到父树的根节点。 下图说明了树的这种递归定义。使用树的递归定义,我们知道下图中的树至少有四个节点,因为表示一个子树的每个三角形必须有一个根节点。 它可能有比这更多的节点,但我们不知道,除非我们更深入树。
# 实现树:节点链接法
使用节点和引用表示树。在这种情况下,我们将定义一个具有根值属性的类,以及左和右子树。使用节点和引用表示树,树结构类似于下图所示。

我们将从节点和引用方法的一个简单的类定义开始,如下方代码所示。要记住这个表示重要的事情是 left 和 right 的属性将成为对 BinaryTree 类的其他实例的引用。 例如,当我们在树中插入一个新的左子节点时,我们创建另一个 BinaryTree 实例,并在根节点中修改self.leftChild 来引用新树节点。
class BinaryTree:
def __init__(self,rootObj):
self.key = rootObj
self.leftChild = None
self.rightChild = None
注意,在上述代码中,构造函数希望获得某种对象以存储在根中。树的根对象可以是对任何对象的引用。
接下来,我们来构建插入左节点的函数。为了向树中添加一个左子树,我们将创建一个新的二叉树对象,并设置根节点的left属性来引用该新对象。insertLeft的代码如下所示 ,
'''Class BinaryTree'''
def insertLeft(self,newNode):
if self.leftChild == None:
self.leftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
我们必须考虑两种插入情况。 第一种情况,当没有左孩子时,只需向树中添加一个节点。 第二种情况是现有左孩子的节点。在这种情况下,我们插入一个节点并将现有的子节点放到树中的下一个层。
同样的,定义插入右节点的函数。insertRight的代码如下所示 ,
'''Class BinaryTree'''
def insertRight(self,newNode):
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
为了完成一个简单二叉树数据结构的定义,接下来将实现获取左和右孩子以及设置和获取值的方法。代码如下,
'''Class BinaryTree'''
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def setRootVal(self,obj):
self.key = obj
def getRootVal(self):
return self.key
现在我们已经拥有创建和操作二叉树的所有内容,现在让我们使用它们来检查结构。
我们创建一个简单的树,以节点a为根,并添加节点b和c作为子节点。完整的代码如下,
class BinaryTree:
def __init__(self,rootObj):
self.key = rootObj
self.leftChild = None
self.rightChild = None
# 插入左子节点
def insertLeft(self,newNode):
if self.leftChild == None:
self.leftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
# 插入右子节点
def insertRight(self,newNode):
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
# 获取左子节点
def getLeftChild(self):
return self.leftChild
# 获取右子节点
def getRightChild(self):
return self.rightChild
# 设置节点携带的值
def setRootVal(self,obj):
self.key = obj
# 获取节点携带的值
def getRootVal(self):
return self.key
r = BinaryTree('a')
print(r.getRootVal())
print(r.getLeftChild())
r.insertLeft('b')
print(r.getLeftChild())
print(r.getLeftChild().getRootVal())
r.insertRight('c')
print(r.getRightChild())
print(r.getRightChild().getRootVal())
r.getRightChild().setRootVal('Hello')
print(r.getRightChild().getRootVal())
# 输出
a
None
<__main__.BinaryTree object at 0x0000022292A9B550>
b
<__main__.BinaryTree object at 0x0000022292A9B860>
c
Hello
